Các dạng bài tập tìm cực trị của hàm số bậc 3 thường gặp

Trong những bài toán về cực trị nằm ở câu hỏi phụ của câu hỏi khảo sát hàm số hết sức đa dạng và thì các bài toán cực trị của hàm số bậc 3 là 1 trong những dạng toán phổ biến nhất. Sau đây chúng ta cùng nghiên cứu về các bài toán cực trị của hàm số bậc 3

1/ Các dạng bài toán về cực trị của hàm số bâc 3

Bài toán tổng quát: Cho hàm số bậc 3 có dạng y = f(x) = ax³ + bx² + cx + d (với a ≠ 0, a, b, c, d phụ thuộc vào tham số). Hãy tìm giá trị của tham số để hàm số y có cực đại hoặc cực tiểu (nói cách khác là cực trị) thỏa mãn điều kiện bài toán cho trước.

Phương pháp giải bài toán cực trị của hàm số bậc 3:

Bước 1:

Tính đạo hàm của hàm số y’ = 3ax² + 2bx + c,

Cho y’ = 0  ⇔ 3ax² +2bx + c = 0 (1)

Để hàm số đã cho có cực đại và cực tiểu  ⇔ y’ = 0 phải có hai nghiệm phân biệt  ⇔ (1) phải có hai nghiệm phân biệt

Ta có a ≠ 0 và ∆ (∆’) ≠ 0 ⇔ Giá trị tham số cần tìm thuộc 1 miền D nào đó (*)

Bước 2:

Từ điều kiện bài toán cho trước ta có 1 phương trình hoặc 1 bất phương trình theo tham số cần tìm

Giải phương trình này ta sẽ tìm được tham số rồi sau đó đối chiếu với điều kiện (*) của tham số và kết luận.

Một số điều kiện của bài toán thường gặp:

– Để hàm số y = f(x) đã cho có 2 cực trị <=> a ≠ 0 và ∆_y’ (∆’) > 0

– Để hàm số y = f(x) đã cho có 2 cực trị nằm về hai phía đối nhau của trục hoành <=> y_CD.y_CT < 0

– Để hàm số y = f(x) đã cho có 2 cực trị nằm về hai phía đối nhau của trục tung <=> x_CD.x_CT < 0

– Để hàm số y = f(x) đã cho có 2 cực trị cùng nằm phía trên của trục hoành <=> 

– Để hàm số  y = f(x) đã cho có 2 cực trị cùng nằm phía dưới của trục hoành <=> 

– Để hàm số  y = f(x) đã cho có cực trị nằm tiếp xúc với trục hoành <=> y_CD.y_CT = 0

– Đồ thị hàm số có 2 điểm cực trị khác nằm phía đối với đường thẳng d có dạng: Ax + By + C = 0

Gọi M₁ (x₁ ; y₁) và M₂ (x₂ ; y₂) là điểm cực đại và điểm cực tiểu của hàm số y = f(x)

Ta có t₁ và t₂ là giá trị của các điểm cực trị M₁, M₂ khi ta thay vào đường thẳng d.

t₁ = Ax₁ + By₁ + C

t₂ = Ax₂ + By₂ + C

Nếu đồ thì có 2 điểm cực trị nằm 2 phía đường thẳng d thì ta có phương trình 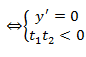 có 2 nghiệm phân biệt x₁, x₂

Nếu đồ thì có 2 điểm cực trị nằm cùng 1 phía đường thẳng d thì ta có phương trình 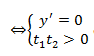 có 2 nghiệm phân biệt x₁, x₂

Chú ý: Khi ta thay đường thẳng d bằng trục của Ox hoặc Oy hay 1 đường tròn thì ta vẫn áp dụng được kết quả trên . Các kết quả khác của nó thì tùy theo từng điều kiện để có thể áp dụng.

2 / Bài tập ví dụ

Bài 1: cho hàm số y = x³ – 2(m + 1)x² + (m² – 3m + 2)x + 4. Tìm m để hàm số có cực đại, cực tiểu và 2 cực trị này nằm về hai phía của trục tung.

Giải:

Tập xác định R

Ta có y’ = 3x² – 2(m + 1)x + (m² – 3m + 2)

Để hàm số có điểm cực đại, cực tiểu nằm về hai phía của trục tung thì phương trình y’ = 0 phải có 1 nghiệm phân biệt

Bài 2: Cho hàm số y = (m +  2)x³ + 3x²  + mx -5 với m là tham số. Tìm giá trị của m để các cực trị có hoành độ là số dương.

Giải:

Tập xác đinh R

Để các cực trị của hàm số có hoành đồ là số dương thì phương trình y’ = 0 có 2 nghiệm phân biệt

Ta có y’ = 3(m + 2)x² + 6x + m

Vậy với -3 < m< -2 thì hàm số đã cho có điểm cực trị có hoành độ là dương

Bài 3: Cho hàm số y = -x³ + 3x² + 3(m² – 1)x – 3m² – 1 (m là tham số thực). Tìm m để hàm số có cực đại, cực tiểu và các điểm cực đại, cực tiểu này cách đều gốc tọa độ O.

Giải:

Ta có đạo hàm y’ = – 3x² + 6x + 3(m² – 1),

y’ = 0 ⇔ – 3x² +6x + 3(m² – 1) = 0 (1)

Để hàm số có cực trị ⇔ y’ = 0 có 2 nghiệm phân biệt

⇔Δ’= m² > 0 ⇔ m ≠ 0

Khi đó ta có tọa độ hai điểm cực trị là A(1 – m, – 2 – m²) và B(1+m ; -2 + 2m²)

Theo giả thiết đề bài 2 điểm cực trị này cách đều gốc tọa độ ta có

⇔ OA = OB

⇔ (1 – m)² + (-2 – 2m²)² = (1+ m)² + (2 – 2m²)²

⇔4m³ = m

⇔ m = ± ½

Vậy với m = ± ½ thì hàm số có cực đại và cực tiểu thỏa mãn hai điểm này cách đều gốc tọa độ O.