I. Tính tích phân bằng phương pháp phân tích
1/ Phương pháp tính tích phân:
Đối với phương pháp phân tích này thì việc sử dụng các đồng nhất thức để có thể biến đổi các biểu thức dưới dấu tích phân thành dạng tổng các hạng tử mà có nguyên hàm của mỗi hạng tử có thể nhận được từ bảng các nguyên hàm hoặc là bằng các phép biển đổi đơn giản mà chúng ta đã biết, sau đó ta áp dụng định nghĩa để giải bài toán này
2/ Ví dụ:
Tính các tích phân sau:
Cách giải
a/ Ta có:
= (ln2 + 1) – (ln1 + 2) = ln2 -1
b/ Ta có
= (24 – 4e) – (0 – 4) = 28 – 4e
II/ Phương pháp tính tích phân bằng đổi biến số
Để tính tích phân bằng phương pháp đổi biến số ta có:
Chọn x = g(t), trong đó ta có g(t) là 1 hàm số khi đó .
Lấy vi phân của hàm số dx
Ta có biểu thị f(x)dx theo t và dt. Ta giả sử f(x)dx = g(t)dt
Ta cần tính các cận tương ứng của hàm số theo a và b
Khi đó I = ? đây chính là tích phân mà chúng ta cần tính.
Đôi khi ta có thể đặt t = v(x) thay vì đặt x = g(t), rồi lấy vi phân 2 vế rồi tính dx theo t sau đó ta tiếp tục làm các bước còn lại như trên. Như vậy việc đặt ẩn phụ là rất đa dạng, căn cứ vào tính chất của hàm dưới dấu tích phân thì có khi nó còn phụ thuộc vào cận a và b nữa.
1/ Dạng 1:
Tính 
với hàm số f(x) liên tục trên đoạn [a ; b]
a/ Phương pháp tính tích phân:
Đặt t = u(x) => d(t) = u'(x)dx (trong đó t = u(x) có đạo hàm liên tục và f(t) liên tục trên tập xác định của t)
Ta cần đổi : 
Ta chuyển đổi tích phân đã cho sang dạng tích phân có tùy biến theo t ta có:
Lưu ý:
- Nếu tích phân có dạng f(x) có chứa (1/x ; lnx) thì ta cần đặt t = lnx
- Nếu tích phân có dạng f(x) mà có chứa
thì ta cần đặt t = u(x) - Nếu hàm số f(x) có dạng mẫu số thì ta cần đặt t = mẫu số
b/ ví dụ:
Tính tích phân của hàm số sau: 
Giải
Ta đặt t = lnx => ta có dt = dx/x
với x = e ta có t = 1 => x = e² => t=2
=> I =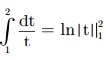 
= ln2
Vậy ta có I = ln2
2/ Tính tích phân bằng phương pháp đổi biến số dạng 2
Cho hàm số: với hàm số f(x) liên tục trên đoạn [a ; b]
a/ Phương pháp giải:
- Ta cần đặt x = φ(t) và d(x) = φ(t)d(t). Trong đó ta có φ(t) là hàm số thích hợp và ảnh φ(t) nằm trong tập xác định của f(x), φ'(t) liên tục trên tập xác định đó.
- Đổi cận của hàm số:
- Biến đổi tích phân I đã cho sang dạng biến t ta được:
Chú ý:
Nếu hàm số f(x) có chứa
thì ta cần đặt x = |a|.sin t với t ∈ [-π/2 ; π/2] và x = |a|.cos t với t ∈ (0 ; π)
thì ta cần đặt x = |a|.tan t với t ∈ [-π/2 ; π/2] và x = |a|.cot t với t ∈ (0 ; π)
thì ta cần đặt x = |a| / sin t hoặc x = |a| / cos t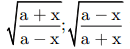
thì ta cần đặt x = a. cos 2t
thì ta cần đặt x = a + (b-a). sin²t
b/ ví dụ
Tính tích phân của hàm số sau: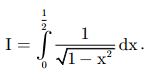 
Giải:
Ta đặt x = sin t với t ∈ [-π/2 ; π/2] ta có => d(x) = cost.dt
Với x = 0 ta có => t = 0
Với x = 1/2 ta có => t = π/6
Khi đó:
Vậy I = π/6
III/ Tính tích phân bằng phương pháp vi phân
Cho hàm số y = f(x) được xác định trên tập D có vi phân của hàm số được ký hiệu là dy = f'(x) .dx hay d(f(x)) = f'(x) .dx
Để giải bài toán dạng này ta cần lưu ý các công thức sau:
- d(ax + b) = a.dx ⇔ dx = d(ax + b) / a (với a ≠ 0)
- d(sinx) = cosx.dx ⇔ dx = d(sinx) / cosx và d(cosx) = – sinx.dx ⇔ dx = d(cosx) / – sinx
IV/ Tính tích phân bằng phương pháp tích phân từng phần
1/ Cách giải:
Ta có công thức của tích phân từng phần
hoặc:
Đặt 
Ta thay vào công thức tính tích phân từng phần trên có:
Chú ý:
- Đặt u = f(x) và dv = g(x). dx hoặc ngược lại sao cho ta có thể dễ dàng tìm nguyên hàm của v(x) và vi phân của d(u) = u'(x). dx mà không quá phức tạp
- Ta cần phải tính được tích phân:
- Trường hợp đặc biệt
a/ Nếu tích phân có dạng: 
Ta đặt u = P(x) với P(x) là đa thức
b/ Nếu cần tính tích phân có dạng:
Ta cần đặt u = ln x
c/ Nếu cần tính tích phân có dạng:
Thì ta phải tính tích phân từng phần 2 lần và đặt u = 
2/ Ví dụ:
Tính tích phân sau: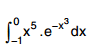 
Giải:
Đặt t = – x³ ⇒ dt = -3x²dx
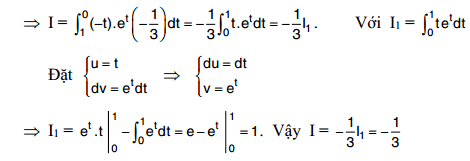
V/ Phương pháp tính tích phân sử dụng tính chẵn lẻ và tính liên tục của hàm số
- Nếu hàm số f(x) lẻ và liên tục trên đoạn [-a ; a] với a > 0 ta có:
- Nếu hàm số f(x) chẵn và liên tục trên đoạn [-a ; a] với a > 0 ta có:
- Nếu hàm số f(x) chẵn và liên tục trên R ta có:
với a ∈ R+ và a > 0
- Nếu f(x) liên tục trên [a ; b] thoả mãn f(x) = f( a +b – x) thì ta có:
Trên đây là tổng hợp các phương pháp tính tích phân. Hi vọng bài viết mang lại cho các bạn những kiến thức bổ ích
