Tìm cực trị của hàm số là 1 dạng bài tập rất quan trọng và thường xuyên gặp trong các đề thi ĐH – THPT QG môn Toán nhất là vào những năm gần đây. Bài viết hôm nay sẽ giúp các bạn có thể hình dung được các bước tìm cực trị của hàm số 1 cách tổng quát và dễ nhớ nhất để các bạn có thể áp dụng.
1/ Phương pháp tìm cực trị của hàm số
Kiến thức cần nhớ để tìm cực trị của hàm số
Cho hàm số y = f(x) ta có:
- Hàm số y = f(x) có điểm cực trị <=> ta có đạo hàm y’ đổi dấu
- Hàm số y = f(x) không có điểm cực trị <=> ta có đạo hàm y’ không đổi dấu
- Hàm số y = f(x) chỉ có 1 điểm cực trị <=> ta có đạo hàm y’ đổi dấu 1 lần
- Hàm số y = f(x) chỉ có 2 điểm cực trị <=> ta có đạo hàm y’ đổi dấu 2 lần
- Hàm số y = f(x) có 3 điểm cực trị <=> ta có đạo hàm y ‘ đổi dấu 3 lần
- Hàm số y = f(x) đạt giá trị cực đại tại điểm x0 nếu:

- Hàm số y = f(x) đạt giá trị cực tiểu tại điểm x0 nếu:

- Hàm số y = f(x) có đạo hàm và đạt cực trị tại điểm x0 nếu f’(x0) = 0
- Hàm số y = f(x) có đạo hàm và đạt giá trị cực trị bằng c tại điểm x0 nếu

Chú ý: Đối với 1 hàm số bất kỳ thì hàm số chỉ đạt cực trị tại điểm mà tại đó đạo hàm của hàm số bị triệt tiêu hoặc đạo hàm của hàm số không xác định.
2/ Tìm cực trị của hàm số bậc 4 trùng phương
Cho hàm số y = ax4 + bx2 + c
Ta có y’ = 4ax3 + 2bx
Cho y’ = 0 ⇔ 4ax3 + 2bx = 0 => 2x (2ax2 + b) = 0

Hàm số đã cho có 3 điểm cực trị khi phương trình trên có (2ax2 + b) = 0 có hai nghiệm phân biệt khác 0 => a.b < 0
Hàm số có 1 nghiệm khi (2ax2 + b) = 0 vô nghiệm hoặc có nghiệm kép và bằng 0
=> 
Nếu ta có đồ thị của hàm số bậc 4 trùng phương có 3 điểm cực trị thì 3 điểm cực trị này luôn luôn tạo ra một tam giác cân có đỉnh nằm trên trục tung.
3/ Cực trị của hàm số hữu tỉ
Cho hàm số có dạng 
Ta có y’ = 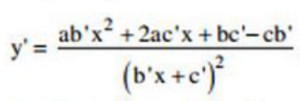
y’ = 0 ta có f(x) = ab’x2 + 2ac’x + bc’– cb’ = 0 (b’x + c’ ≠ 0)
Hàm số có điểm cực đại, cực tiểu ó y’ = 0 có 2 nghiệm phân biệt khi đó ta có
ab’ ≠ 0 và ∆f > 0
Khi f(x) = 0 có 2 nghiệm thì 2 nghiệm này thỏa mãn điều kiện b’x + c’ ≠ 0
Hàm số không có điểm cực trị khi y’= 0 vô nghiệm hoặc có nghiệm kép
Đồ thị của hàm số có 2 điểm cực trị cùng 1 phía Ox khi
ab’ ≠ 0, ∆f > 0 và ycđ.yct > 0 (hoặc ab’ ≠ 0, ∆f > 0 và y’ = 0 có 2 nghiệm phân biệt)
Đồ thị của hàm số có 2 điểm cực trị nằm 2 phía Ox khi
ab’ ≠ 0, ∆f > 0 và ycđ.yct < 0 (hoặc ab’ ≠ 0 và y’ = 0 vô nghiệm)
4/ Bài tập
Bài 1: Cho hàm số y = x4 – 2(m + 1)x2 + m (1) với m là tham số
Tìm m để cho đồ thị hàm số (1) có 3 điểm cực trị là A,B,C sao cho OA = BC lấy O là gốc tọa độ A là điểm cực trị nằm trên trục tung, B và C là 2 điểm cực trị còn lại.
Giải:
Ta có y’ = 4x3 – 4(m + 1)x
Cho y’ = 0 ó 4x3 – 4(m + 1)x = 0
x = 0 và x2 = m+1
hàm số có 3 điểm cực trị khi 4x3 – 4(m + 1)x = 0 có 3 nghiệm
m + 1 > 0 ⇔ m > -1
Khi m > -1 thì y’= 0 thì x = 0 và x = ![]()
Ta có A (0 ; m) 
Theo giả thuyết ta có OA = BC => m2 = 4m + 1 => m = ![]()
Vậy với m = ![]() hàm số có 3 điểm cực trị
hàm số có 3 điểm cực trị
Bài 2: cho hàm số y = x4 -2m2x2 + 1. Tìm m để đồ thị của hàm số có 3 điểm cực trị A, B, C tạo thành tam giác có diện tích là 32
Giải:
Ta có y’ = 4x3 – 4m2x
Với y’ = 0 ta có x = 0 và x2 = m2
Để hàm số có 3 điểm cực trị thì m ≠ 0
ta có tọa độ của 3 điểm cực trị là
A (0 ; 1) , B (-m ; 1 – m4) và C (m ; 1 – m4)
Ta cần chứng minh tam giác ABC cân tại đỉnh A
tọa độ trung điểm I của cạnh BC là (0 ; 1 – m4)
Ta có SABC = ½ AI.BC = m4 . |m| = |m|5 = 32
m = ± 2
Vậy với m = ± 2 thì hàm số đã cho có 3 cực trị tạo thành tam giác có diện tích là 32
