Bài toán viết phương trình tiếp tuyến của đồ thị hàm số là 1 trong những bài toán quan trọng nó thường xuất hiện trong các đề thi tốt nghiệp, đề thi đại học nhiều năm gần đây. Các bạn cần lưu ý nhiều đến dạng toán này để có thể giúp các bạn có bài thì tốt nhất và có những điểm số cao nhất.
1/ Kiến thức lưu ý khi giải bài toán viết phương trình tiếp tuyến.
Định nghĩa tiếp tuyến là gì?. Theo các giải thích đơn giản và dễ hiểu thì:
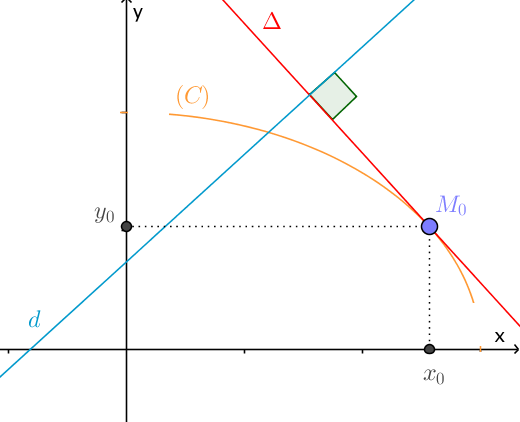
Giả sử ta có 1 hàm số y=f(x) có đồ thị là 1t đường cong ký hiệu là (C), 1 đường thẳng d tiếp xúc với đường cong (C) tại điểm M(x0 ; y0) được gọi là tiếp tuyến của (C) tại điểm M đó.

Ta có “d tiếp xúc với (C)”, vậy ta cần giải thích như thế nào là tiếp xúc? Hình vẽ bên trên có thể giúp ta phân biết giữa tiếp xúc và cắt.
Ta có đường thẳng d tiếp xúc với đường cong (C) tại điểm M và cắt đường cong (C) tại điểm N.
Khi đó điểm M(x0 ; y0) gọi là tiếp điểm của tiếp tuyến d và đồ thị (c). Điển M thuộc đồ thị hàm số y=f(x) nên ta có y0= ƒ( x0).
Khi đó ta có hệ số góc của tiếp tuyến d tại điểm y0= ƒ( x0) chính là đạo hàm của hàm số y=f(x) tại điểm này. Vậy ta có được phương trình tiếp tuyến:
y – y0 = ƒ'( x0)(x-x0)
Trong 1 bài toán về viết phương trình tiếp tuyến, chúng ta chỉ cần tìm được tọa độ của tiếp điểm (x0 ; y0) và hệ số góc ƒ'( x0) là ta có thể viết được phương trình tiếp tuyến này.
2/ Các dạng bài toán viết phương trình tiếp tuyến cơ bản
Dạng 1: Viết phương trình tiếp tuyến của hàm số khi biết tọa độ tiếp điểm.
Với dạng bài toán này này ta chỉ cần tính hệ số góc là có thể viết được phương trình tiếp tuyến.
Bài tập ví dụ: Viết phương trình tiếp tuyến của đồ thị hàm số sau y = ƒ(x)= x³ – 2x + 1 tại điểm M(2 ; 5).
Giải
Khi đó ta có:ƒ'(x) = 3x² – 2
Hệ số góc của tiếp tuyến tại điểm M(2 ; 5) : ƒ'(2) = 3.2² – 2 = 10
Phương trình tiếp tuyến của đồ thị là: y – 5 = 10(x – 2) <=> y = 10x – 15
Dạng 2: Viết phương trình tiếp tuyến của hàm số khi biết hoành độ giao điểm.
Với dạng bài toàn này ta đã biết được x0 , cần tìm thêm y0 và hệ số góc = ƒ'(x0) của hàm số
Bài tạp ví dụ: Hãy viết phương trình tiếp tuyến của đồ thị hàm số sau: y = ƒ(x)= x³ – 2x + 1 tại 1 điểm có hoành độ bằng 1.
Giải
Khi đó ta có: ƒ'(x) = 3x² – 2
Gọi điểm N(x0 ; y0) là tiếp điểm của tiếp tuyến đó và đồ thị hàm số.
Khi đó ta có: x0 = 1 => y0 =ƒ(1) =0
Hệ số góc của tiếp tuyến là: ƒ'(1) = 3.2¹ – 2 = 1
Vậy ta có phương trình tiếp tuyến: y – 0 = 1(x – 1) <=> y = x – 1
Dạng 3: Viết phương trình tiếp tuyến của hàm số biết tung độ tiếp điểm.
Với dạng bài toán này ta đã biết được y0 . Ta cần đi tìm x0 và hệ số góc của hàm số.
Bài tập ví dụ: Hãy viết phương trình tiếp tuyến của đồ thị hàm số sau: y = ƒ(x)= x³ + 2x + 1 tại 1 điểm có tung độ bằng 1.
Giải
Ta có : ƒ'(x) = 3x² + 2
Gọi điểm M(x0 ; y0) là tiếp điểm của tiếp tuyến với đồ thị hàm số.
Theo đề bài:
Hệ số góc của tiếp tuyến là : ƒ'(0) = 3.(0)² + 2 = 2
Vậy ta có phương trình tiếp tuyến: y – 1 = 2(x – 0) => y = 2x + 1
Dạng 4: Viết phương trình tiếp tuyến khi biết hệ số góc của tiếp tuyến.
Với dạng toán này ta cần tìm tọa độ của tiếp điểm để có thể viết được phương trình tiếp tuyến.
Bài tập ví dụ: Viết phương trình tiếp tuyến đồ thị hàm số sau y = ƒ(x)= x³ + 2x + 1 cho biết hệ số góc của tiếp tuyến bằng 5.
Giải
Ta có: ƒ'(x) = 3x² + 2
Gọi điểm M(x0 ; y0) là tiếp điểm của tiếp tuyến với đồ thị hàm số.
Khi đó ta có hệ số góc của tiếp tuyến là: ƒ'(x0) = 5 <=> 3x0² + 2 = 5 <=> x0 = ±1
Với x0 = 1 , y0 = 4 thì phương trình tiếp tuyến: y – 4 = 5(x – 1) => y = 5x – 1
Với x0 = -1 , y0 = – 2 thì phương trình tiếp tuyến: y + 2 = 5(x + 1) => y = 5x + 3
Lưu ý: với dạng toán này có thể cho ở dạng viết phương trình tiếp tuyến của hàm số khi biết tiếp tuyến song song hoặc vuông góc với 1 đường thẳng cho trước. Khi đó ta cần sử dụng các nhận xét sau để tìm hệ số góc của tiếp tuyến này:
- Nếu 2 đường thẳng song song với nhau thì hai hệ số góc bằng nhau.
- Nếu 2 đường thẳng vuông góc với nhau thì tích hai hệ số góc bằng -1.
Nếu đường thẳng có phương trình là y = ax + b thì ta có hệ số góc là k = a.
Bài tập ví dụ: Hãy viết phương trình tiếp tuyến của đồ thị hàm số có dạng y = ƒ(x)= x³ + 2x + 1 cho biết tiếp tuyến vuông góc với đường thẳng d có dạng – 2x + y – 1 = 0: .
Giải
Ta có: ƒ'(x) = 3x² + 2
Từ đường thẳng d ta có: – 2x + y – 1 = 0 => y= 2x + 1
Vậy hệ số góc của d là . k(d) = 2
Gọi điểm M(x0 ; y0) là tiếp điểm của tiếp tuyến và đồ thị. Vậy hệ số góc của tiếp tuyến là ƒ'(x0) .
Vì tiếp tuyến vuông góc với d ta có:
ƒ'(x0).k(d) = – 1 <=> ƒ'(x0).2 = – 1 <=> ƒ'(x0) = – 1/2 <=> 3x0² + 2 = -1/2
(phương trình này vô nghiệm)
Vậy không có tiếp tuyến nào thỏa yêu cầu bài toán.
Trên đây là một số dạng toán viết phương trình tiếp tuyến cơ bản các bạn cần nắm được trước khi tiếp cận với các dạng toán khó hơn trong tuyển tập các đề thi tuyển sinh đại học.

